|
|
@@ -348,7 +348,7 @@ value, and what value we decided on.
|
|
|
|
|
|
The first parameter to decide on, is the $\sigma$ used in the Gaussian blur. To
|
|
|
find this parameter, we tested a few values, by trying them and checking the
|
|
|
-results. It turned out that the best value was $\sigma = 1.1$.
|
|
|
+results. It turned out that the best value was $\sigma = 1.4$.
|
|
|
|
|
|
\subsection{Parameter \emph{cell size}}
|
|
|
|
|
|
@@ -377,7 +377,13 @@ are not significant enough to allow for reliable classification.
|
|
|
The neighbourhood to use can only be determined through testing. We did a test
|
|
|
with each of these neighbourhoods, and we found that the best results were
|
|
|
reached with the following neighbourhood, which we will call the
|
|
|
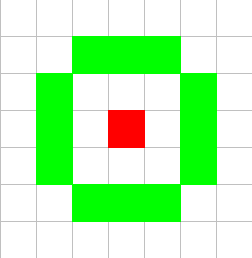
-()-neighbourhood.
|
|
|
+(12, 5)-neighbourhood, since it has 12 points in a area with a diameter of 5.
|
|
|
+
|
|
|
+\begin{figure}[H]
|
|
|
+\center
|
|
|
+\includegraphics[scale=0.5]{12-5neighbourhood.png}
|
|
|
+\caption{(12,5)-neighbourhood}
|
|
|
+\end{figure}
|
|
|
|
|
|
\subsection{Parameters $\gamma$ \& $c$}
|
|
|
|
|
|
@@ -398,8 +404,41 @@ checks for each combination of values what the score is. The combination with
|
|
|
the highest score is then used as our parameters, and the entire SVM will be
|
|
|
trained using those parameters.\\
|
|
|
\\
|
|
|
-We found that the best values for these parameters are $c = ?$ and
|
|
|
-$\gamma = ?$.
|
|
|
+The results of this grid-search are shown in the following table. The values
|
|
|
+in the table are rounded percentages, for easy displaying.
|
|
|
+
|
|
|
+\begin{tabular}{|r|r r r r r r r r r r|}
|
|
|
+\hline
|
|
|
+c $\gamma$ & $2^{-15}$ & $2^{-13}$ & $2^{-11}$ & $2^{-9}$ & $2^{-7}$ &
|
|
|
+ $2^{-5}$ & $2^{-3}$ & $2^{-1}$ & $2^{1}$ & $2^{3}$\\
|
|
|
+\hline
|
|
|
+$2^{-5}$ & 61 & 61 & 61 & 61 & 62 &
|
|
|
+ 63 & 67 & 74 & 59 & 24\\
|
|
|
+$2^{-3}$ & 61 & 61 & 61 & 61 & 62 &
|
|
|
+ 63 & 70 & 78 & 60 & 24\\
|
|
|
+$2^{-1}$ & 61 & 61 & 61 & 61 & 62 &
|
|
|
+ 70 & 83 & 88 & 78 & 27\\
|
|
|
+ $2^{1}$ & 61 & 61 & 61 & 61 & 70 &
|
|
|
+ 84 & 90 & 92 & 86 & 45\\
|
|
|
+ $2^{3}$ & 61 & 61 & 61 & 70 & 84 &
|
|
|
+ 90 & 93 & 93 & 86 & 45\\
|
|
|
+ $2^{5}$ & 61 & 61 & 70 & 84 & 90 &
|
|
|
+ 92 & 93 & 93 & 86 & 45\\
|
|
|
+ $2^{7}$ & 61 & 70 & 84 & 90 & 92 &
|
|
|
+ 93 & 93 & 93 & 86 & 45\\
|
|
|
+ $2^{9}$ & 70 & 84 & 90 & 92 & 92 &
|
|
|
+ 93 & 93 & 93 & 86 & 45\\
|
|
|
+$2^{11}$ & 84 & 90 & 92 & 92 & 92 &
|
|
|
+ 92 & 93 & 93 & 86 & 45\\
|
|
|
+$2^{13}$ & 90 & 92 & 92 & 92 & 92 &
|
|
|
+ 92 & 93 & 93 & 86 & 45\\
|
|
|
+$2^{15}$ & 92 & 92 & 92 & 92 & 92 &
|
|
|
+ 92 & 93 & 93 & 86 & 45\\
|
|
|
+\hline
|
|
|
+\end{tabular}
|
|
|
+
|
|
|
+We found that the best values for these parameters are $c = 32$ and
|
|
|
+$\gamma = 0.125$.
|
|
|
|
|
|
\section{Results}
|
|
|
|
|
|
@@ -415,7 +454,17 @@ measure the time used to classify a license plate, not the training of the
|
|
|
dataset, since that can be done offline, and speed is not a primary necessity
|
|
|
there.\\
|
|
|
\\
|
|
|
-The speed of a classification turned out to be ???.
|
|
|
+The speed of a classification turned out to be reasonably good. We time between
|
|
|
+the moment a character has been 'cut out' of the image, so we have a exact
|
|
|
+image of a character, to the moment where the SVM tells us what character it is.
|
|
|
+This time is on average $65$ ms. That means that this
|
|
|
+technique (tested on an AMD Phenom II X4 955 Quad core CPU running at 3.2 GHz)
|
|
|
+can identify 15 characters per second.\\
|
|
|
+\\
|
|
|
+This is not spectacular considering the amount of calculating power this cpu
|
|
|
+can offer, but it is still fairly reasonable. Of course, this program is
|
|
|
+written in Python, and is therefore not nearly as optimized as would be
|
|
|
+possible when written in a low-level language.
|
|
|
|
|
|
\subsection{Accuracy}
|
|
|
|
|
|
@@ -426,16 +475,31 @@ accuracy score we possibly can.\\
|
|
|
\footnote{
|
|
|
\url{http://en.wikipedia.org/wiki/Automatic_number_plate_recognition}},
|
|
|
commercial license plate recognition software score about $90\%$ to $94\%$,
|
|
|
-under optimal conditions and with modern equipment. Our program scores an
|
|
|
-average of ???.
|
|
|
+under optimal conditions and with modern equipment.\\
|
|
|
+\\
|
|
|
+Our program scores an average of $93\%$. However, this is for a single
|
|
|
+character. That means that a full license plate should theoretically
|
|
|
+get a score of $0.93^6 = 0.647$, so $64.7\%$. That is not particularly
|
|
|
+good compared to the commercial ones. However, our focus was on getting
|
|
|
+good scores per character, and $93\%$ seems to be a fairly good result.\\
|
|
|
+\\
|
|
|
+Possibilities for improvement of this score would be more extensive
|
|
|
+grid-searches, finding more exact values for $c$ and $\gamma$, more tests
|
|
|
+for finding $\sigma$ and more experiments on the size and shape of the
|
|
|
+neighbourhoods.
|
|
|
|
|
|
\section{Conclusion}
|
|
|
|
|
|
In the end it turns out that using Local Binary Patterns is a promising
|
|
|
-technique for License Plate Recognition. It seems to be relatively unsensitive
|
|
|
+technique for License Plate Recognition. It seems to be relatively indifferent
|
|
|
for the amount of dirt on license plates and different fonts on these plates.\\
|
|
|
\\
|
|
|
-The performance speedwise is ???
|
|
|
+The performance speed wise is fairly good, when using a fast machine. However,
|
|
|
+this is written in Python, which means it is not as efficient as it could be
|
|
|
+when using a low-level languages.
|
|
|
+\\
|
|
|
+We believe that with further experimentation and development, LBP's can
|
|
|
+absolutely be used as a good license plate recognition method.
|
|
|
|
|
|
\section{Reflection}
|
|
|
|