"worked on LBP explanation"

docs/verslag.tex

@@ -1,6 +1,8 @@
 \documentclass[a4paper]{article}
 
+\usepackage{amsmath}
 \usepackage{hyperref}
+\usepackage{graphicx}
 
 \title{Using local binary patterns to read license plates in photographs}
 
@@ -101,13 +103,71 @@ will always be of the same height, and the character will alway be positioned
 at either the left of right side of the image.
 
 \subsection{Local binary patterns}
-
 Once we have separate digits and characters, we intent to use Local Binary
-Patterns to determine what character or digit we are dealing with. Local Binary
+Patterns (Ojala, Pietikäinen \& Harwood, 1994) to determine what character
+or digit we are dealing with. Local Binary
 Patters are a way to classify a texture based on the distribution of edge
 directions in the image. Since letters on a license plate consist mainly of
 straight lines and simple curves, LBP should be suited to identify these.
 
+\subsubsection{LBP Algorithm}
+The LBP algorithm that we implemented is a square variant of LBP, the same
+that is introduced by Ojala et al (1994). Wikipedia presents a different
+form where the pattern is circular. 
+\begin{itemize}
+\item Determine the size of the square where the local patterns are being
+registered. For explanation purposes let the square be 3 x 3. \\
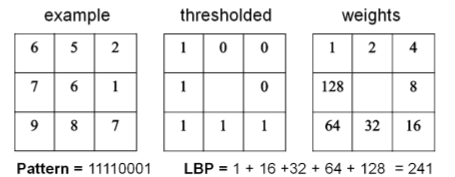
+\item The grayscale value of the middle pixel is used a threshold. Every value of the pixel 
+around the middle pixel is evaluated. If it's value is greater than the threshold
+it will be become a one else a zero.
+
+\begin{figure}[h!]
+\center
+\includegraphics[scale=0.5]{lbp.png}
+\caption{LBP 3 x 3 (Pietik\"ainen, Hadid, Zhao \& Ahonen (2011))}
+\end{figure}
+
+Notice that the pattern will be come of the form 01001110. This is done when a the value
+of the evaluated pixel is greater than the threshold, shift the bit by the n(with i=i$_{th}$ pixel
+evaluated, starting with $i=0$).
+
+This results in a mathematical expression:
+Let I($x_i, y_i$) an Image with grayscale values and $g_n$ the grayscale value of the pixel $(x_i, y_i)$. 
+Also let $s(g_i - g_c)$ with $g_c$ = grayscale value of the center pixel.
+
+$$
+  s(v, g_c) = \left\{
+  \begin{array}{l l}
+    1 & \quad \text{if v $\geq$ $g_c$}\\
+    0 & \quad \text{if v $<$ $g_c$}\\
+  \end{array} \right.
+$$
+
+$$LBP_{n, g_c = (x_c, y_c)} = \sum\limits_{i=0}^{n-1} s(g_i, g_c)^{2i} $$
+
+The outcome of this operations will be a binary pattern.
+
+\item Given this pattern, the next step is to divide the pattern in cells. The
+amount of cells depends on the quality of the result, so trial and error is in order.
+Starting with dividing the pattern in to 16 cells. 
+
+\item Compute a histogram for each cell.
+
+\pagebreak
+\begin{figure}[h!]
+\center
+\includegraphics[scale=0.7]{cells.png}
+\caption{Divide in cells(Pietik\"ainen et all (2011))}
+\end{figure}
+
+\item Consider every histogram as a vector element and concatenate these. The result is a
+feature vector of the image.
+
+\item Feed these vectors to a support vector machine. This will ''learn'' which vector
+are. 
+
+\end{itemize}
+
 To our knowledge, LBP has yet not been used in this manner before. Therefore,
 it will be the first thing to implement, to see if it lives up to the
 expectations. When the proof of concept is there, it can be used in the final